rlauxe

rlauxe (“r-lux”)

WORK IN PROGRESS last changed: 12/25/2025

A library for Risk Limiting Audits (RLA), based on Philip Stark’s SHANGRLA framework and related code. The Rlauxe library is an independent implementation of the SHANGRLA framework, based on the published papers of Stark et al.

The SHANGRLA python library is the work of Philip Stark and collaborators, released under the AGPL-3.0 license.

Rlauxe uses the Raire Java library for Ranked Choice contests, also called Instant runoff Voting (IRV). Raire-Java is Copyright 2023-2025 Democracy Developers. It is based on software (c) Michelle Blom in C++ https://github.com/michelleblom/audit-irv-cp/tree/raire-branch , and released under the GNU General Public License v3.0.

Also see:

Click on plot images to get an interactive html plot. You can also read this document on github.io.

Table of Contents

SHANGRLA framework

SHANGRLA is a framework for running Risk Limiting Audits for elections. It uses a statistical risk testing function that allows an audit to statistically prove that an election outcome is correct (or not) to within a risk level α. For example, a risk limit of 5% means that the election outcome (i.e. the winner(s)) is correct with 95% probability.

It uses an assorter to assign a number to each ballot, and checks outcomes by testing half-average assertions, each of which claims that the mean of a finite list of numbers is greater than 1/2. The complementary null hypothesis is that the assorter mean is not greater than 1/2. If that hypothesis is rejected for every assertion, the audit concludes that the outcome is correct. Otherwise, the audit expands, potentially to a full hand count. If every assertion is tested at risk level α, this results in a risk-limiting audit with risk limit α: if the election outcome is not correct, the chance the audit will stop shy of a full hand count is at most α.

term definition
Nc a trusted, independent bound on the number of valid cards cast in the contest c.
Ncast the number of ballot cards validly cast in the contest
risk we want to confirm or reject the null hypothesis with risk level α.
assorter assigns a number between 0 and upper to each card, chosen to make assertions “half average”.
assertion the mean of assorter values is > 1/2: “half-average assertion”
estimator estimates the true population mean from the sampled assorter values.
bettingFn decides how much to bet for each sample. (BettingMart)
riskFn the statistical method to test if the assertion is true.
audit iterative process of choosing ballots and checking if all the assertions are true.

Audit Workflow Overview

Before the Audit

For each contest:

Create the Card Manifest:

Committment:

Creating a random seed

Starting the Audit

The Election Auditors (EA) can examine the audit committment files, run simulations to estimate how many cards will need to be sampled, etc. The EA can choose:

The audit configuration parameters are written to auditConfig.json.

Audit Rounds

The audit proceeds in rounds:

  1. Estimation: for each contest, estimate how many samples are needed to satisfy the risk limit
  2. Choosing contests and sample sizes: the EA decides which contests and how many samples will be audited. This may be done with an automated algorithm, or the Auditor may make individual contest choices.
  3. Random sampling: The actual ballots to be sampled are selected in order from the sorted Manifest until the sample size is satisfied.
  4. Manual Audit: find the chosen paper ballots that were selected to audit and do a manual audit of each.
  5. Create MVRs: enter the results of the manual audits (as Manual Vote Records, MVRs) into the system.
  6. Run the audit: For each contest, using the MVRs, calculate if the risk limit is satisfied.
  7. Decide on Next Round: for each contest not satisfied, decide whether to continue to another round, or call for a hand recount.

Each round generates samplePrns.json, sampleCards.csv, sampleMvrs.csv, and auditState.json files, which become part of the Audit Record.

Verification

Independently written verifiers can read the Audit Record and verify that the audit was correctly performed.

Audit Types

In all cases:

Card Level Comparison Audits (CLCA)

When the election system produces an electronic record for each ballot card, known as a Cast Vote Record (CVR), then Card Level Comparison Audits can be done that compare sampled CVRs with the corresponding hand audited ballot card, known as the Manual Vote Record (MVR). A CLCA typically needs many fewer sampled ballots to validate contest results than other methods.

The requirements for CLCA audits:

For the risk function, rlauxe uses the BettingMart function with the GeneralAdaptiveBetting betting function. GeneralAdaptiveBetting uses estimates/measurements of the error rates between the Cvrs and the Mvrs. If the error estimates are correct, one gets optimal “sample sizes”, the number of ballots needed to prove the election is correct.

See CLCA Risk function for details on the BettingMart risk function.

See Generalized Adaptive Betting for CLCA for details on the GeneralAdaptiveBetting function.

OneAudit CLCA

OneAudit is a type of CLCA audit, based on the ideas and mathematics of the ONEAudit papers (see appendix). It deals with the cases where:

  1. CVRS are not available for all ballots, and the remaining ballots are in one or more “pools” for which subtotals are available. (This is the Boulder “redacted votes” case.)
  2. CVRS are available for all ballots, but some cannot be matched to physical ballots. (This is the San Francisco case where mail-in ballots have matched CVRS, and in-person precinct votes have unmatched CVRs. Each precinct’s ballots are kept in a separate pool.)

In both cases we create an “overstatement-net-equivalent” (ONE) CVR for each pool, and use the average assorter value in that pool as the value of the (missing) CVR in the CLCA overstatement. When a ballot has been chosen for hand audit:

  1. If it has a CVR, use the standard CLCA over-statement assorter value for the ballot.
  2. If it has no CVR, use the overstatement-net-equivalent (ONE) CVR from the pool that it belongs to.

Thus, all cards must either have a CVR or be contained in a pool.

For results, see OneAudit results.

For details of use cases, see OneAudit Use Cases.

Polling Audits

When CVRs are not available, a Polling audit can be done instead. A Polling audit
creates an MVR for each ballot card selected for sampling, just as with a CLCA, except without the CVR.

For the risk function, Rlaux uses the AlphaMart (aka ALPHA) function with the ShrinkTrunkage estimation of the true population mean (theta). ShrinkTrunkage uses a weighted average of an initial estimate of the mean with the measured mean of the mvrs as they are sampled. The reported mean is used as the initial estimate of the mean.

See AlphaMart risk function for details on the AlphaMart risk function.

Comparing Samples Needed by Audit type

Here we look at the actual number of samples needed to reject or confirm the risk limit (aka samplesNeeded). We ignore the need to estimate a batch size, as if we do “one sample at a time”. In the section Estimating Sample Batch sizes below, we deal with the need to estimate a batch size, and the extra overhead that brings.

In general, samplesNeeded is independent of N. Instead, samplesNeeded depends on the diluted margin as well as the random sequence of ballots chosen to be hand audited.

(Actually there is a slight dependence on N for “without replacement” audits when the sample size approaches N, but that case approaches a full hand audit, and isnt very interesting.)

The following plots are simulations, averaging the results from the stated number of runs.

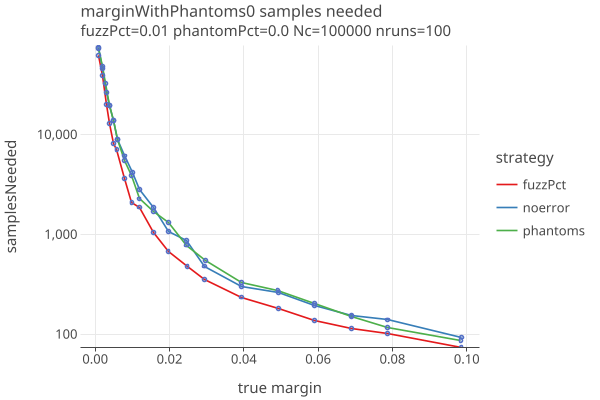
Samples needed with no errors

The audit needing the least samples is CLCA when there are no errors in the CVRs, and no phantom ballots. In that case, the samplesNeeded depend only on the margin, and is a straight line vs margin on a log-log plot.

The best case for CLCA no-errors is when you always make the maximum bet of 2. However, if it turns out there are errors, the maximum bet will “stall” the audit and you wont recover. To deal with this, rlauxe sets a maximum bet allowed. Here is a plot of CLCA no-error audits with maximum risks of 70, 80, 90, and 100% maximum:

clcaNoErrorsMaxRiskLogLog

Currently we set maximum risk to 90%, and we are investigating what the optimal setting should be.

In any setting of maximum risk, the CLCA assort value is always the same when there are no errors, and so there is no variance.

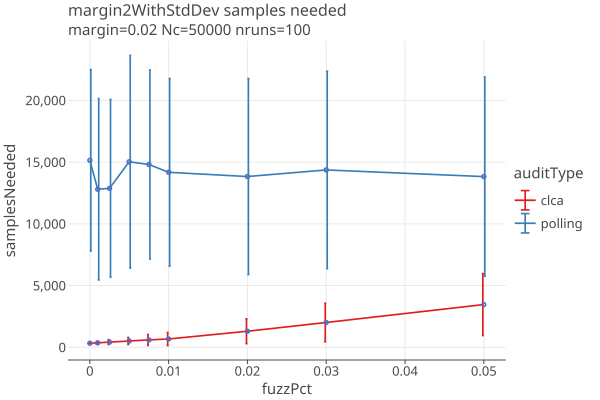
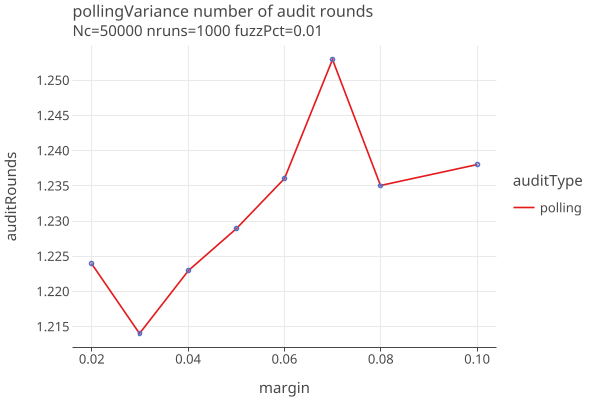
For polling, the assort values vary, and the number of samples needed depends on the order the samples are drawn. Here we show the average and standard deviation over 100 independent trials at each reported margin, when no errors are found:

pollingWithStdDev

Samples needed when there are errors

In the following simulations, errors are created between the CVRs and the MVRs, by taking fuzzPct of the ballots and randomly changing the candidate that was voted for. When fuzzPct = 0.0, the CVRs and MVRs agree. When fuzzPct = 0.01, 1% of the contest’s votes were randomly changed, and so on.

With the margin fixed at 4%, this plot compares polling and CLCA audits and their variance:

margin2WithStdDevLinear

In this plot we show CLCA audits with margins of .01, .02, and .04, over a range of fuzz errors from 0 to 1%:

clcaAuditsWithFuzz

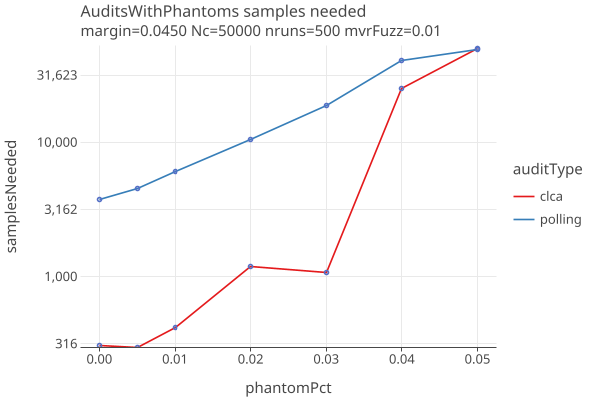
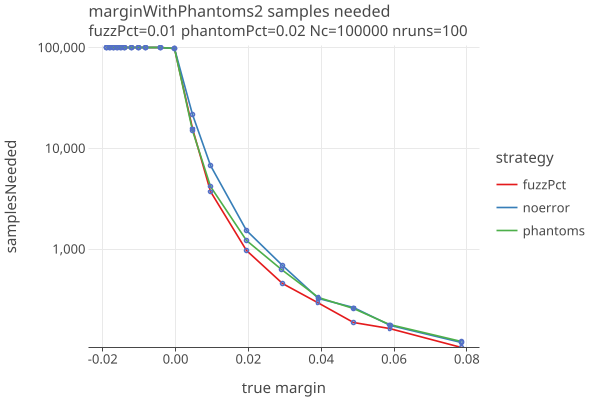
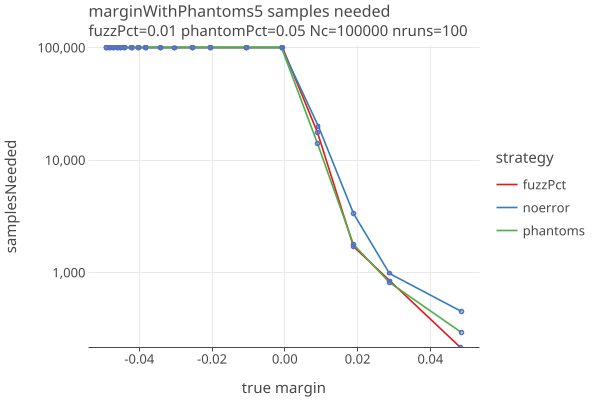
Effect of Phantoms on Samples needed

Varying phantom percent, up to and over the margin of 4.5%, with errors generated with 1% fuzz:

auditsWithPhantomsLogLinear

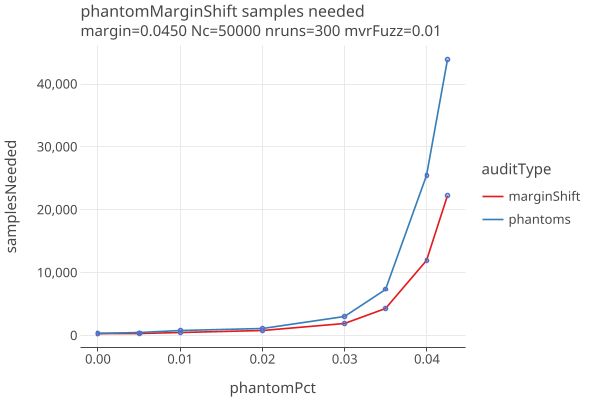
Having phantomPct phantoms is similar to subtracting phantomPct from the margin. In this CLCA plot we show samples needed as a function of phantomPct, and also with no phantoms but the margin shifted by phantomPct:

phantomMarginShiftLinear

Sample Populations and diluted margins

Once we have all of the contests’ estimated sample sizes, we next choose which ballots/cards to sample. This step depends on the CardManifest and Population information, which tells which cards have which contests. When you know exactly what contests are on each card, the contest margin is at a maximum, and the samplesNeeded are at a minimum. If you dont know exactly what contests are on each card, the cards may be divided up into populations in a way that minimizes the number of cards that might have the contest. See SamplePopulations for more explanation and current thinking.

For CLCA audits, the generated Cast Vote Records (CVRs) comprise the Card Style Data, as long as the CVR records the undervotes (contests where no vote was cast). For Polling audits and OneAudit pools, the Populations describe which contests are on which cards.

Estimating Sample Batch sizes

Sampling refers to choosing which ballots to hand review to create Manual Voting Records (MVRs). Once the MVRs are created, the actual audit takes place.

Audits are done in rounds. The auditors must decide how many cards/ballots they are willing to audit, since at some point its more efficient for them to do a full handcount than the more elaborate process of tracking down a subset that has been selected for the sample. Theres a tradeoff between the overall number of ballots sampled and the number of rounds, but, we would like to minimize both.

Note that in this section we are plotting nmvrs = overall number of ballots sampled, which includes the inaccuracies of the estimation. Above we have been plotting samples needed, as if we were doing “one ballot at a time” auditing.

There are two phases to sampling: estimating the sample batch sizes for each contest, and then randomly choosing ballots that contain at least that many contests.

Estimation

For each contest we simulate the audit with manufactured data that has the same margin as the reported outcome, and a guess at the error rates.

For each contest assertion we run auditConfig.nsimEst (default 100) simulations and collect the distribution of samples needed to satisfy the risk limit. We then choose the (auditConfig.quantile) sample size as our estimate for that assertion, and the contest’s estimated sample size is the maximum of the contest’s assertion estimates.

If the simulation is accurate, the audit should succeed auditConfig.quantile fraction of the time (default 80%). Since we dont know the actual error rates, or the order that the errors will be sampled, these simulation results are just estimates.

Note that each round does its own sampling without regard to the previous round’s results. However, since the seed remains the same, the ballot ordering is the same throughout the audit. We choose the lowest ordered ballots first, so previously audited MVRS are always used again in subsequent rounds, for contests that continue to the next round. At each round we record both the total number of MVRs, and the number of “new samples” needed for that round, which are the ballots the auditors have to find and hand audit for that round.

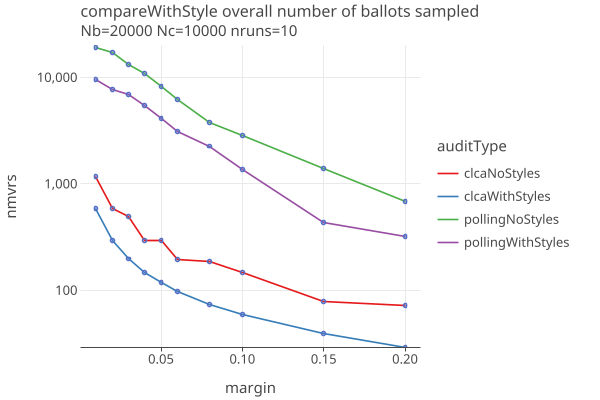
Polling Vs CLCA with/out CSD

The following plot shows nmvrs for Polling vs CLCA, with and without CSD at different margins, no errors, where Nb/Nc = 2.

compareWithStyleLogLinear

Under/Over estimating CLCA sample sizes

Overestimating sample sizes uses more hand-counted MVRs than needed. Underestimating sample sizes forces more rounds than needed. Over/under estimation is strongly influenced by over/under estimating error rates.

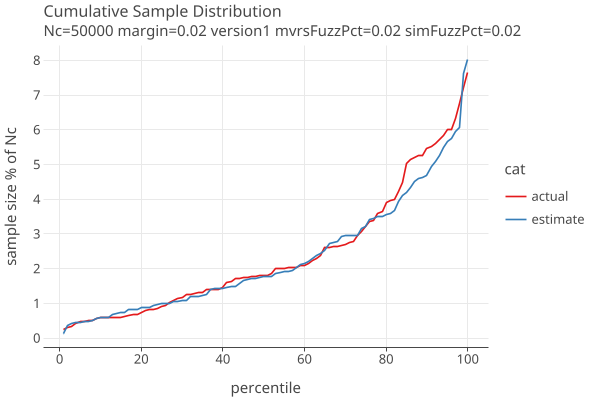
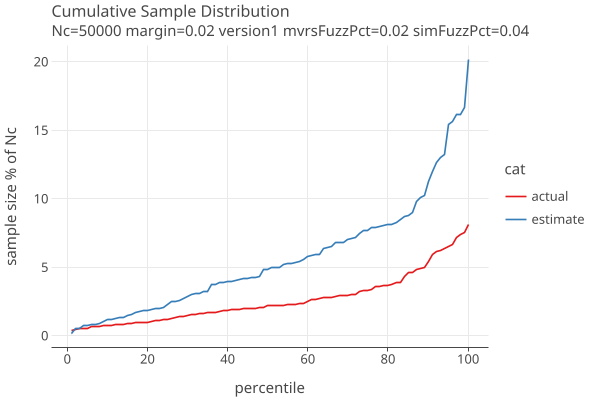
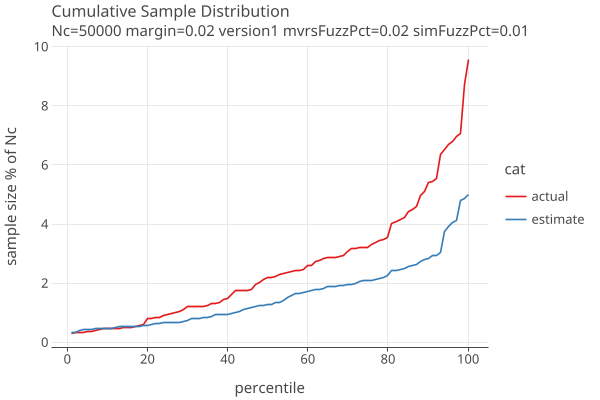
The following plots show approximate distribution of estimated and actual sample sizes, using our standard AdaptiveBetting betting function with weight parameter d = 100, for margin=2% and errors in the MVRs generated with 2% fuzz.

When the estimated error rates are equal to the actual error rates:

estErrorRatesEqual

When the estimated error rates are double the actual error rates:

estErrorRatesDouble

When the estimated error rates are half the actual error rates:

estErrorRatesHalf

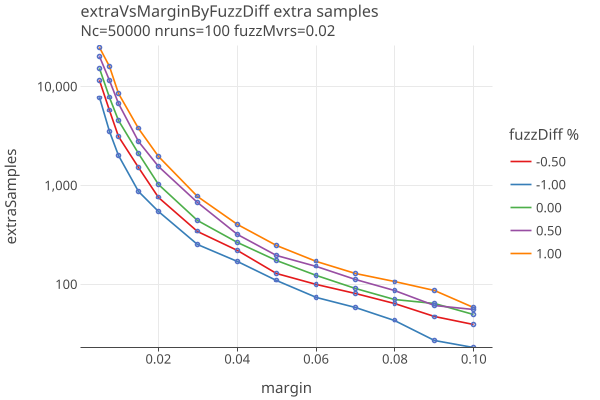
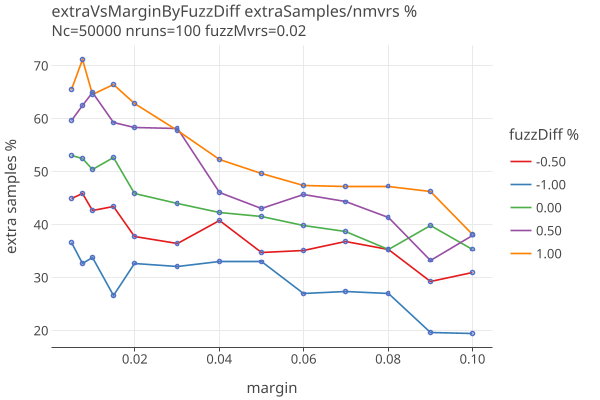
The amount of extra sampling closely follows the number of samples needed, adding around 30-70% extra work, as the following plots vs margin show:

extraVsMarginByFuzzDiffLogLinear extraVsMarginByFuzzDiffPct

The “extra samples” goes up as our guess for the error rates differ more from the actual rates. In these plots we use fuzzPct as a proxy for what the error rates might be.

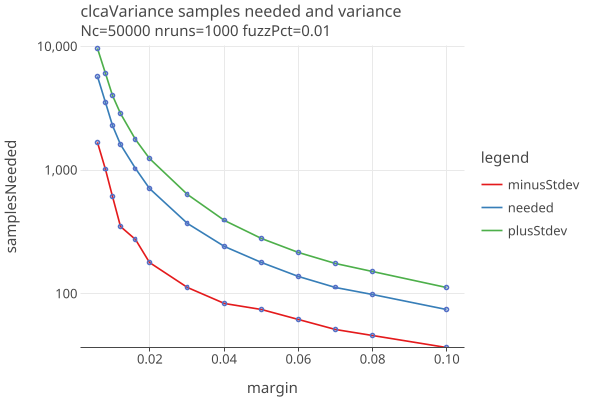
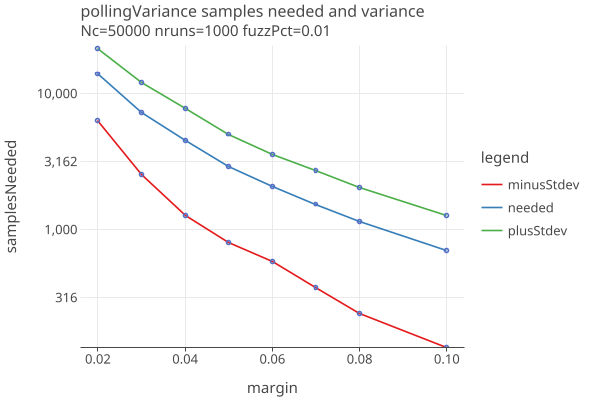
In the best case, the simulation accurately estimates the distribution of audit sample sizes (fuzzDiff == 0%). But because there is so much variance in that distribution, the audit sample sizes are significantly overestimated. To emphasize this point, here are plots of average samples needed, and samples needed +/- one stddev, one for CLCA and one for polling:

clcaVarianceLogLinear pollingVarianceLogLinear

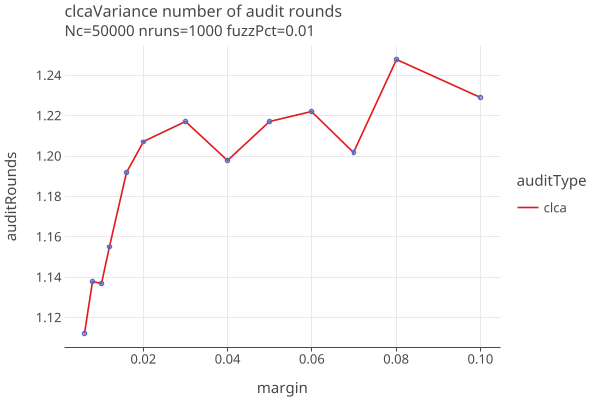
The number of rounds needed reflects the default value of auditConfig.quantile = 80%, so we expect to need a second round 20% of the time:

clcaVarianceNrounds pollingVarianceNrounds

Multiple Contest Auditing

An election often consists of several or many contests, and it is likely to be more efficient to audit all of the contests at once. We have several mechanisms for choosing contests to remove from the audit to keep the sample sizes reasonable.

Before the audit begins:

  1. Any contest whose reported margin is less than auditConfig.minMargin is removed from the audit with failure code MinMargin.
  2. Any contest whose reported margin is less than its phantomPct (Np/Nc) is removed from the audit with failure code TooManyPhantoms.

For each Estimation round:

  1. Any contest whose estimated samplesNeeded exceeds auditConfig.sampleCutoff is removed from the audit with failure code FailMaxSamplesAllowed.
  2. If the total number of ballots for a multicontest audit exceeds auditConfig.sampleCutoff, the contest with the largest estimated samplesNeeded is removed from the audit with failure code FailMaxSamplesAllowed. The Consistent/Uniform sampling is then redone without that contest, and the check on the total number of ballots is repeated.

These rules are somewhat arbitrary but allow us to test audits without human intervention. In a real audit, auditors might hand select which contests to audit, interacting with the estimated samplesNeeded from the estimation stage, and try out different scenarios before committing to which contests continue on to the next round.

Efficiency

We assume that the cost of auditing a ballot is the same no matter how many contests are on it. So, if two contests always appear together on a ballot, then auditing the second contest is “free”. If the two contests appear on the same ballot some pct of the time, then the cost is reduced by that pct. More generally the reduction in cost of a multicontest audit depends on the various percentages the contests appear on the same ballot.

Deterministic sampling order for each Contest

For any given contest, the sequence of ballots/CVRS to be used by that contest is fixed when the PRNG is chosen.

In a multi-contest audit, at each round, the estimate of the number of ballots needed for each contest is calculated = n, and the first n ballots in the contest’s sequence are sampled. The total set of ballots sampled in a round is just the union of the individual contests’ set. The extra efficiency of a multi-contest audit comes when the same ballot is chosen for more than one contest.

The set of contests that will continue to the next round is not known, so the set of ballots sampled at each round is not known in advance. Nonetheless, for each contest, the sequence of ballots seen by the algorithm is fixed when the PRNG is chosen.

Attacks

Attacks are scenarios where the actual winner is not the reported winner. They may be intentional, due to malicious actors, or unintentional, due to mistakes in the process or bugs in the software.

Attack with phantoms

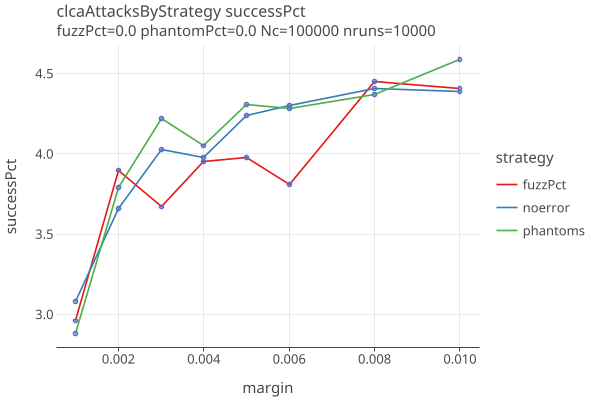
Here we investigate what happens when the percentage of phantoms is high enough to flip the election, but the reported margin does not reflect that. In other words an attack (or error) when the phantoms are not correctly reported.

We create CLCA simulations at different margins and percentage of phantoms, and fuzz the MVRs at 1%. We measure the “true margin” of the MVRs, including phantoms, by applying the CVR assorter, and use that for the x axis.

The error estimation strategies in this plot are:

These are just the initial guesses for the error rates. In all cases, they are adjusted as samples are made and errors are found.

Here are plots of sample size as a function of true margin, for phantomPct of 0, 2, and 5 percent:

marginWithPhantoms0LogLinear marginWithPhantoms2LogLinear marginWithPhantoms5LogLinear

Attack with wrong reported winner

Here we investigate an attack when the reported winner is different than the actual winner.

We create simulations at the given reported margins, with no fuzzing or phantoms. Then in the MVRs we flip just enough votes to make the true margin < 50%. We want to be sure that the percent of false positives stays below the risk limit (here its 5%):

clcaAttacksByStrategyFalsePositives

Appendices

Reference Papers

P2Z         Limiting Risk by Turning Manifest Phantoms into Evil Zombies. Banuelos and Stark. July 14, 2012
    https://arxiv.org/pdf/1207.3413
    
RAIRE        Risk-Limiting Audits for IRV Elections. Blom, Stucky, Teague 29 Oct 2019
    https://arxiv.org/abs/1903.08804

SHANGRLA     Sets of Half-Average Nulls Generate Risk-Limiting Audits: SHANGRLA.	Stark, 24 Mar 2020
    https://arxiv.org/pdf/1911.10035, https://github.com/pbstark/SHANGRLA

MoreStyle	More style, less work: card-style data decrease risk-limiting audit sample sizes. Glazer, Spertus, Stark; 6 Dec 2020
    https://arxiv.org/abs/2012.03371
    
Proportional  Assertion-Based Approaches to Auditing Complex Elections, with Application to Party-List Proportional Elections; 2 Oct, 2021
    Blom, Budurushi, Rivest, Stark, Stuckey, Teague, Vukcevic
    http://arxiv.org/abs/2107.11903v2
    
ALPHA:      Audit that Learns from Previously Hand-Audited Ballots. Stark, Jan 7, 2022
    https://arxiv.org/pdf/2201.02707, https://github.com/pbstark/alpha.

BETTING     Estimating means of bounded random variables by betting. Waudby-Smith and Ramdas, Aug 29, 2022
    https://arxiv.org/pdf/2010.09686, https://github.com/WannabeSmith/betting-paper-simulations

COBRA:      Comparison-Optimal Betting for Risk-limiting Audits. Jacob Spertus, 16 Mar 2023
    https://arxiv.org/pdf/2304.01010, https://github.com/spertus/comparison-RLA-betting/tree/main

ONEAudit:   Overstatement-Net-Equivalent Risk-Limiting Audit. Stark 6 Mar 2023.
    https://arxiv.org/pdf/2303.03335, https://github.com/pbstark/ONEAudit

STYLISH	    Stylish Risk-Limiting Audits in Practice. Glazer, Spertus, Stark  16 Sep 2023
    https://arxiv.org/pdf/2309.09081, https://github.com/pbstark/SHANGRLA

SliceDice   Dice, but don’t slice: Optimizing the efficiency of ONEAudit. Spertus, Glazer and Stark, Aug 18 2025
    https://arxiv.org/pdf/2507.22179; https://github.com/spertus/UI-TS
    
Verifiable  Risk-Limiting Audits Are Interactive Proofs — How Do We Guarantee They Are Sound?
    Blom, Caron, Ek, Ozdemir, Pereira, Stark, Teague, Vukcevic
    submitted to IEEE Symposium on Security and Privacy (S&P 2026 Cycle 2)

Also see complete list.

Extensions of SHANGRLA

Populations and hasStyle

Rlauxe uses Population objects as a way to capture the information about which cards are in which sample populations, in order to set the diluted margins correctly. This allows us to refine SHANGRLA’s hasStyle flag. See SamplePopulations for more explanation and current thinking.

CardManifest

Rlauxe uses a CardManifest, which consists of a canonical list of AuditableCards, one for each possible card in the election, and the list of Populations. OneAudit pools are subtypes of Populations. The CardManifest is one of the committments that the Prover must make before the random seed can be generated.

General Adaptive Betting strategy.

SHANGRLA’s Adaptive Betting Strategy has been generalized to work for both CLCA and OneAudit and for any assorter. It uses estimated and/or measured error rates to set optimal betting values. This is currently the only betting strategy used by Rlauxe. See GeneralizedAdaptiveBetting for more info.

MaxRisk for Betting

In order to prevent stalls in BettingMart, the maximum bet is bounded by a “maximum risk” value, which is the maximum percent of your “winnings” you are willing to risk on any one bet.

Additional assorters

Dhondt, AboveThreshold and BelowThreshold assorters have been added to support Belgian elections using Dhondt proportional scoring. These assorters have an upper bound != 1, so are an important generalization of the Plurality assorter.

OneAudit Card Style Data

Rlauxe adds the option that there may be CSD for OneAudit pooled data, in part to investigate the difference between having CSD and not. Specifically, different OneAudit pools may have different values of hasStyle (aka hasSingleCardStyle). See SamplePopulations.

Developer Notes

Modules

Also See: